Support | Portal
Statistical Methods and Terminology
Statistical Calculations
Statistical analyses are performed on the log-transformed batch-normalized, imputed data using Metabolon’s internal pipeline, which uses R (http://cran.r-project.org/) to perform statistical computations via a Jupyter Notebooks user interface. Below are examples of frequently employed significance tests and classification methods followed by a discussion of p- and q-value significance thresholds.
Welch’s two-sample t-test
A Welch’s two-sample t-test is used to test whether two unknown means are different from two independent populations.
This version of the two-sample t-test allows for unequal variances (variance is the square of the standard deviation) and has an approximate t-distribution with degrees of freedom estimated using Satterthwaite’s approximation. We typically use a two-sided test (tests whether the means are different) instead of a one-sided test (tests whether one mean is greater than the other).
Two-way ANOVA
When performing an analysis of variance (ANOVA) significance test, it is assumed that variance is the same across all populations.
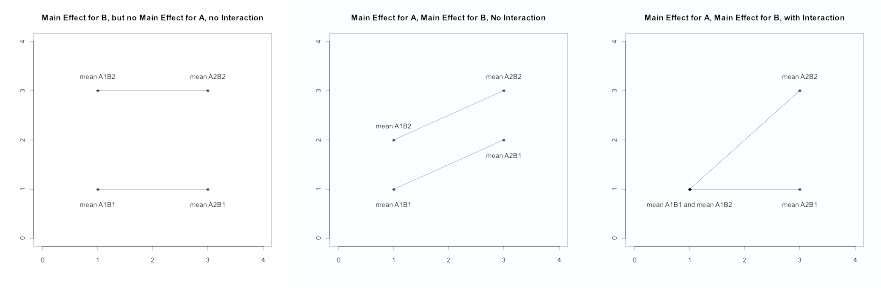
In a two-way ANOVA, three statistical tests are typically performed: the main effect of each factor individually and that of the interaction. Suppose we have two factors, A and B, where A represents the genotype and B represents diet in a mouse study. Suppose each of these factors has two levels (A: wild type, knock out; B: standard diet, high-fat diet). In this example, there are four possible combinations (“treatments”): A1B1, A1B2, A2B1, and A2B2. The overall ANOVA F-test yields the p-value for testing whether all four of these means are equal or whether at least one pair is different.
However, we are also interested in the individual effects of genotype and diet. A main effect is a contrast that tests one factor across all levels of the other factor. Hence the A main effect compares (A1B1 + A1B2)/2 vs. (A2B1 + A2B2)/2, and the B-main effect compares (A1B1 + A2B2)/2 vs. (A1B2 + A2B2)/2. The interaction is a contrast that tests whether the mean difference for one factor depends on the level of the other factor, which is (A1B2 + A2B1)/2 vs. (A1B1 + A2B2)/2.
Some sample plots are shown below. The first plot illustrates a B main effect that does not depend on the level of A, so there is no A main effect and no interaction. In the second plot, the mean difference for B is the same at each level of A, and the mean difference for A is the same at each level of B, indicating the absence of a statistical interaction. The final plot illustrates main effects for A and B as well as an interaction: the effect of B depends on the level of A (0 for A1 but 2 for A2); in other words, the effect of diet depends on the genotype. Additionally, the interpretation of the main effects depends on whether there is an interaction.
p-values
For statistical significance testing, p-values are provided. The lower the p-value, the greater the evidence that the null hypothesis (typically that two population means are equal) is false. If “statistical significance” is declared for p-values less than 0.05, then 5% of the time, the incorrect conclusion that the means are different when actually they are the same is made.
The p-value is the probability that the test statistic is at least as extreme as observed in this experiment, given that the null hypothesis is true. Hence, the more extreme the statistic, the lower the p-value and the more evidence the data give against the null hypothesis.
q-values
A significance level of 0.05 is the false positive rate when there is one test. However, for a large number of tests, false positives need to be accounted for. There are different methods to correct for multiple tests. The oldest methods are family-wise error rate adjustments (Bonferroni, Tukey, etc.), but these tend to be extremely conservative for very large numbers of tests.
With gene arrays, using the False Discovery Rate (FDR) is more common. The family-wise error rate adjustments provide a high degree of confidence that there are zero false discoveries. However, with FDR methods, a small number of false discoveries can be accounted for. The FDR for a given set of compounds can be estimated using the q-value1.
To interpret the q-value, the data must first be sorted by the p-value, then the significance cutoff (typically p < 0.05) must be chosen. The q-value gives the false discovery rate for the selected list (i.e., an estimate of the proportion of false discoveries for the list of compounds whose p-value is below the significance cutoff). In Table 1 below, if the whole list is declared significant, then the false discovery rate is approximately 10%. If everything from Compound 079 and above is declared significant, then the false discovery rate is approximately 2.5%.

Table 1. Example of q-value interpretation.
Instrument and Process Variability
Instrument variability is determined by calculating the median relative standard deviation (RSD) for the internal standards that are added to each sample prior to injection into the mass spectrometers. Overall process variability is determined by calculating the median RSD for all endogenous metabolites (i.e., non-instrument standards) present in 100% of the Client Matrix samples, which are technical replicates of pooled client samples. RSD values can be found within the Heatmap Excell file, downloaded from the “Data &Integration” tab of the portal.
References
- Storey J and Tibshirani R. Statistical significance for genomewide studies. Proc Natl Acad Sci USA 2003;100(16):9440-9445.
Table of Contents
Getting Started
Overview & FAQs
Common How-Tos
Discovery Panel Report
Impact Explorer & Heliogram
Profile Finder
Knowledge Base
Product Glossary
Experimental Procedures
Statistical Methods & Terminology
Data Privacy & Security
Share this page
See how Metabolon can advance your path to preclinical and clinical insights
Contact Us
Talk with an expert
Request a quote for our services, get more information on sample types and handling procedures, request a letter of support, or submit a question about how metabolomics can advance your research.
Corporate Headquarters
617 Davis Drive, Suite 100
Morrisville, NC 27560
Mailing Address:
P.O. Box 110407
Research Triangle Park, NC 27709

