Méthodes statistiques et terminologie

Calculs statistiques

Les analyses statistiques sont effectuées sur les données imputées normalisées par lots et log-transformées à l'aide du pipeline interne de Metabolon, qui utilise R(http://cran.r-project.org/) pour effectuer des calculs statistiques via une interface utilisateur Jupyter Notebooks. Vous trouverez ci-dessous des exemples de tests de signification et de méthodes de classification fréquemment utilisés, suivis d'une discussion sur les seuils de signification des valeurs p et q.

Test t à deux échantillons de Welch

Un test t de Welch à deux échantillons est utilisé pour vérifier si deux moyennes inconnues sont différentes de deux populations indépendantes.

Cette version du test t à deux échantillons tient compte des variances inégales (la variance est le carré de l'écart-type) et présente une distribution t approximative avec des degrés de liberté estimés à l'aide de l'approximation de Satterthwaite. Nous utilisons généralement un test bilatéral (qui vérifie si les moyennes sont différentes) plutôt qu'un test unilatéral (qui vérifie si une moyenne est supérieure à l'autre).

ANOVA à deux voies

Lors d'un test de signification de l'analyse de la variance (ANOVA), on suppose que la variance est la même dans toutes les populations.

Dans une ANOVA à deux voies, trois tests statistiques sont généralement effectués : l'effet principal de chaque facteur individuellement et celui de l'interaction. Supposons que nous ayons deux facteurs, A et B, où A représente le génotype et B le régime alimentaire dans une étude sur la souris. Supposons que chacun de ces facteurs ait deux niveaux (A : type sauvage, knock out ; B : régime standard, régime riche en graisses). Dans cet exemple, il existe quatre combinaisons possibles ("traitements") : A1B1, A1B2, A2B1 et A2B2. Le test F de l'ANOVA globale donne la valeur p pour tester si les quatre moyennes sont égales ou si au moins une paire est différente.

Cependant, nous nous intéressons également aux effets individuels du génotype et du régime alimentaire. Un effet principal est un contraste qui teste un facteur sur tous les niveaux de l'autre facteur. Ainsi, l'effet principal A compare (A1B1 + A1B2)/2 à (A2B1 + A2B2)/2, et l'effet principal B compare (A1B1 + A2B2)/2 à (A1B2 + A2B2)/2. L'interaction est un contraste qui teste si la différence moyenne pour un facteur dépend du niveau de l'autre facteur, soit (A1B2 + A2B1)/2 vs (A1B1 + A2B2)/2.

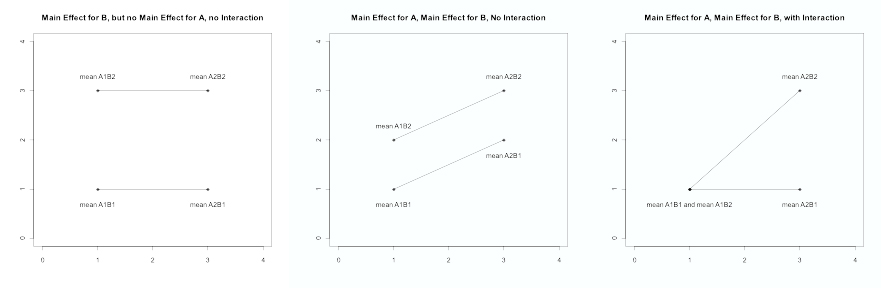
Quelques exemples de graphiques sont présentés ci-dessous. Le premier graphique illustre un effet principal B qui ne dépend pas du niveau de A, il n'y a donc pas d'effet principal A ni d'interaction. Dans le deuxième graphique, la différence moyenne pour B est la même à chaque niveau de A, et la différence moyenne pour A est la même à chaque niveau de B, ce qui indique l'absence d'interaction statistique. Le dernier graphique illustre les effets principaux pour A et B ainsi qu'une interaction : l'effet de B dépend du niveau de A (0 pour A1 mais 2 pour A2) ; en d'autres termes, l'effet du régime alimentaire dépend du génotype. En outre, l'interprétation des effets principaux dépend de l'existence ou non d'une interaction.

Valeurs p

Pour les tests de signification statistique, les valeurs p sont fournies. Plus la valeur p est faible, plus la preuve que l'hypothèse nulle (typiquement que deux moyennes de population sont égales) est fausse est grande. Si la "signification statistique" est déclarée pour des valeurs p inférieures à 0,05, la conclusion erronée selon laquelle les moyennes sont différentes alors qu'elles sont en fait identiques est tirée dans 5 % des cas.

La valeur p est la probabilité que la statistique du test soit au moins aussi extrême que celle observée dans cette expérience, étant donné que l'hypothèse nulle est vraie. Par conséquent, plus la statistique est extrême, plus la valeur p est faible et plus les données vont à l'encontre de l'hypothèse nulle.

valeurs q

Un niveau de signification de 0,05 correspond au taux de faux positifs lorsqu'il n'y a qu'un seul test. Cependant, pour un grand nombre de tests, les faux positifs doivent être pris en compte. Il existe différentes méthodes pour corriger les tests multiples. Les méthodes les plus anciennes sont les ajustements du taux d'erreur par famille (Bonferroni, Tukey, etc.), mais elles tendent à être extrêmement conservatrices pour un très grand nombre de tests.

Avec les réseaux de gènes, l'utilisation du taux de fausse découverte (FDR) est plus courante. Les ajustements du taux d'erreur par famille offrent un degré élevé de certitude qu'il n'y a pas de fausses découvertes. Cependant, avec les méthodes FDR, un petit nombre de fausses découvertes peut être pris en compte. Le FDR pour un ensemble donné de composés peut être estimé à l'aide de la valeur q1.

To interpret the q-value, the data must first be sorted by the p-value, then the significance cutoff (typically p < 0.05) must be chosen. The q-value gives the false discovery rate for the selected list (i.e., an estimate of the proportion of false discoveries for the list of compounds whose p-value is below the significance cutoff). In Table 1 below, if the whole list is declared significant, then the false discovery rate is approximately 10%. If everything from Compound 079 and above is declared significant, then the false discovery rate is approximately 2.5%.

Variabilité des instruments et des processus

La variabilité des instruments est déterminée en calculant l'écart-type relatif médian (RSD) pour les étalons internes qui sont ajoutés à chaque échantillon avant d'être injectés dans les spectromètres de masse. La variabilité globale du processus est déterminée en calculant l'écart-type relatif médian pour tous les métabolites endogènes (c'est-à-dire les étalons non instrumentaux) présents dans 100 % des échantillons de la matrice client, qui sont des réplicats techniques d'échantillons de clients regroupés. Les valeurs RSD se trouvent dans le fichier Heatmap Excell, téléchargé à partir de l'onglet "Data &Integration" du portail.

Références

1. Storey J et Tibshirani R. Statistical significance for genomewide studies. Proc Natl Acad Sci USA 2003;100(16):9440-9445.